
Hey! I'm Spawek, and this is the story of a project I built with my friends to make our LAN parties better.
For the past 16 years, we’ve been organizing at least one LAN party every year with a group of friends. These parties typically last 4-5 days, with around 12 people joining at peak times. It’s not just about gaming - we also enjoy partying, intense discussions (we’re all big nerds), board games, card games like Star Realms, and Mafia. Some people arive later, some leave earlier. Some go to take care of their kids for a while. The LAN party is a place of fun and chill.

It's a LAN party so, we play computer games a lot! Dota 2 is our main game, but we also play classics like Counter-Strike, Wolfenstein: Enemy Territory, Warcraft 3, Blooby Volley, and more.
Selecting teams - especially Dota 2 ones - was always hard for us. We decided to automate the team selection process. It led to a very interesting ideas and a neat solution. But to get there, you will need a bit of a context.
A single Dota 2 match lasts about 40 minutes and is usually played 5v5 (though 6v6 is possible). Unbalanced matches, like 4v5, tend to be one-sided. For us it's just more fun when everyone plays - so often games are unbalanced.
Better players use their skill advantage to level faster and earn more gold (a.k.a. snowball), which makes even small differences between players very noticible.
In our group, around half of us play Dota regularly, while others have only ever played during our LAN parties, so skill differences are huge. There are also some other factors:
To choose teams, we typically have two leaders (usually the best or least experienced players) who pick teammates in alternating turns, much like picking football teams in school.
There’s a twist: the first leader picks one player, the second picks two, then the first leader picks two, and so on, with a single-player choice as each leader’s final pick. This balances the advantage of picking first.
Example with 11 people:
Leaders:
- Spawek (me - leader 1)
- Bixkog (my brother - leader 2)
1st pick - team 1 - 1st pick = 1 player:
- Muhah
2nd pick - team 2 - regular pick = 2 players:
- Alpinus
- Dragon
3rd pick - team 1:
- Vifon
- Goovie
4th pick - team 2:
- Status
- Bania
5th pick - team 1 - last pick = 1 player:
- Hypys
6th pick - team 2 - last pick = 1 player:
- J
| team 1 | team 2 |
|---|---|
| Spawek | Bixkog |
| Muhah | Alpinus |
| Vifon | Dragon |
| Goovie | Status |
| Hypys | Bania |
| J |
As the differences between players are big, this process tends to pick similar or even the same teams each time, which is just boring for us. It doesn't work well when the number of players is uneven.
During the last LAN party, we got frustrated with the process and coded something quickly to automate it.
We found some historical data and put it to Colab (all data and code is there if you want to play yourself).
data = [
{
"winner": ["Dragon", "Spawek", "Status", "Vifon"],
"loser": ["Bixkog", "Alpinus", "Hypys", "J", "Goovie"]
},
{
"winner": ["Bixkog", "Alpinus", "Vifon", "J", "Goovie"],
"loser": ["Dragon", "Hypys", "Spawek", "Status"]
},
{
"winner": ["J", "Hypys", "Spawek", "Status", "Vifon"],
"loser": ["Bixkog", "Dragon", "Goovie", "Alpinus"]
},
# ... (35 games in total)
]
Elo rating is often used in games. Players starts at 1000 Elo points, earning or losing points with each game.
The probability of P1 (player 1) winning with P2 is defined as:
$$ P(P1, P2) = \frac{1}{1 + 10^{\frac{P2-P1}{400}}} $$
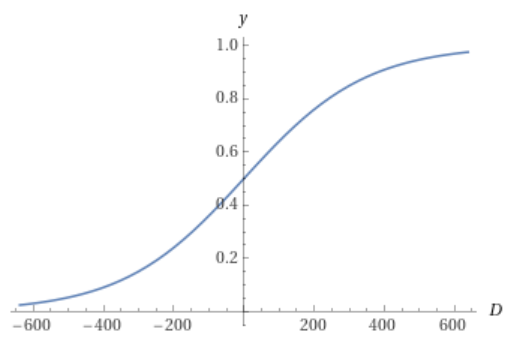
So only the Elo difference between players (D) is relevant:
$$ D = P1 - P2 $$
$$ P(D) = \frac{1}{1 + 10^{\frac{-D}{400}}} $$
The chance of winning is 50% if you have the same Elo as your opponent, 64% if you have 100 Elo more, and 76% if you have 200 Elo more:
To get the Elo of each team, let's simply sum the Elo of all team members:
$$ Elo(team) = \sum_{}^{team}Elo(player) $$
It's obviously problematic for unbalanced teams, but let's start simple.
Let's create the first solution by giving players 20 Elo for winning a match, and taking 20 Elo for losing a match:
from collections import defaultdict
elo = defaultdict(lambda: 1000.0)
for game in data:
for winner in game["winner"]:
elo[winner] += 20.0
for loser in game["loser"]:
elo[loser] -= 20.0
We get some results:
Spawek: 1260
Bixkog: 1140
Dragon: 1100
Bania: 1020
Muhah: 1020
Vifon: 1000
Hypys: 980
Alpinus: 960
Status: 900
Goovie: 900
J: 860
With this, we could generate balanced teams by finding combinations with the smallest Elo difference:
from itertools import combinations
requested_players = ["Hypys", "Spawek", "Bixkog", "Muhah", "J", "Vifon", "Bania", "Goovie"]
best_diff = float('inf')
best_team = None
expected_elo = sum([elo[player] for player in requested_players]) / 2
for team1 in combinations(requested_players, len(requested_players) // 2):
team1 = list(team1)
team1_elo = sum([elo[player] for player in team1])
diff = abs(team1_elo - expected_elo)
if diff < best_diff:
best_diff = diff
team2 = [player for player in requested_players if player not in team1]
team2_elo = sum([elo[player] for player in team2])
best_teams = (team1, team2, team1_elo, team2_elo)
print(f"team 1: {best_teams[0]}, total Elo: {round(best_teams[2])}")
print(f"team 2: {best_teams[1]}, total Elo: {round(best_teams[3])}")
Results:
team 1: ['Hypys', 'Spawek', 'J', 'Vifon'], total Elo: 4100
team 2: ['Bixkog', 'Muhah', 'Bania', 'Goovie'], total Elo: 4080
Woohoo! We've got the first solution!
We only have 35 historical games, so passing through them only once to compute Elo seems like a waste.
In the Elo system, you will get more than 20 points when you win against a player having a higher Elo, same way you will lose less than 20 points if you lose against a player having a higher Elo. For a winner:
$$ update = 40 * (1 - P(win)) $$
The losing player loses exactly the same amount of Elo, that winner gets. E.g.
Spawek (Elo: 1260) wins vs Goovie (Elo: 900):
Spawek += 4.47 Elo
Goovie -= 4.47 Elo
Status (Elo: 900) wins vs Dragon (Elo: 1100):
Status += 30.38 Elo
Dragon -= 30.38 Elo
In colab:
def win_probability(A, B):
elo_diff = A - B
return 1.0 / (1.0 + pow(10.0, (-elo_diff / 400.0)))
def elo_update(winner, loser):
prob = win_probability(winner, loser)
return 40.0 * (1 - win_probability(winner, loser))
As we are using team Elo instead of individual players, let's split the update between all players in the team evenly. Let's go through the data multiple times and see how the results change:
from collections import defaultdict
elo = defaultdict(lambda: 1000.0)
for iteration in range(0, 401):
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
update = elo_update(winner_elo, loser_elo)
for winner in game["winner"]:
elo[winner] += update / len(game["winner"])
for loser in game["loser"]:
elo[loser] -= update / len(game["loser"])
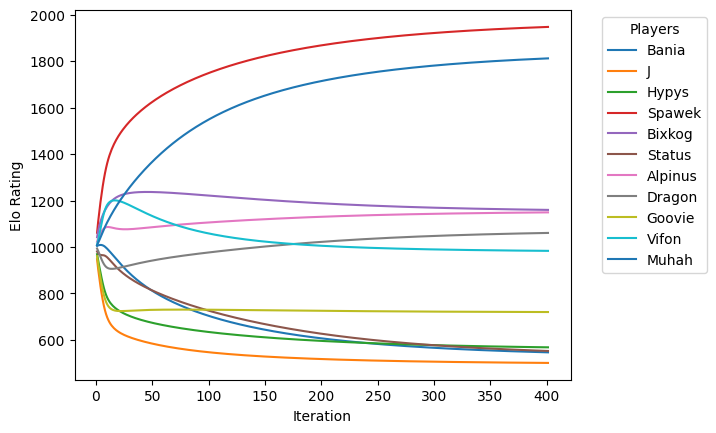
We coded this during the LAN party and it was a really awesome feeling to see that the computations converge! We used that algorithm for the rest of the party, adding new data after each game.
The solution was quite good, but we've seen it creating clearly unbalanced matches from time to time. In such cases, we just added the match with the assumed winner to the data as a "fake game" and generated new teams.
I knew that for the next LAN party, we could do better than that.
Key ideas:
Let's stick to the Elo system we are using. The model will compute Elo for each player. We will compare SUM(Elo) of teams to compute the probability of winning.
Let's define a simple L2 loss function. Our model will try to minimize loss over all games: $$ loss = (\text{real_chance} - \text{predicted_chance})^2 $$
def loss(data, elo):
loss = 0.0
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
computed_probability = win_probability(winner_elo, loser_elo)
real_probability = 1.0
loss += (real_probability - computed_probability)**2.0
return loss
So to compute total loss we have to go over all games and:
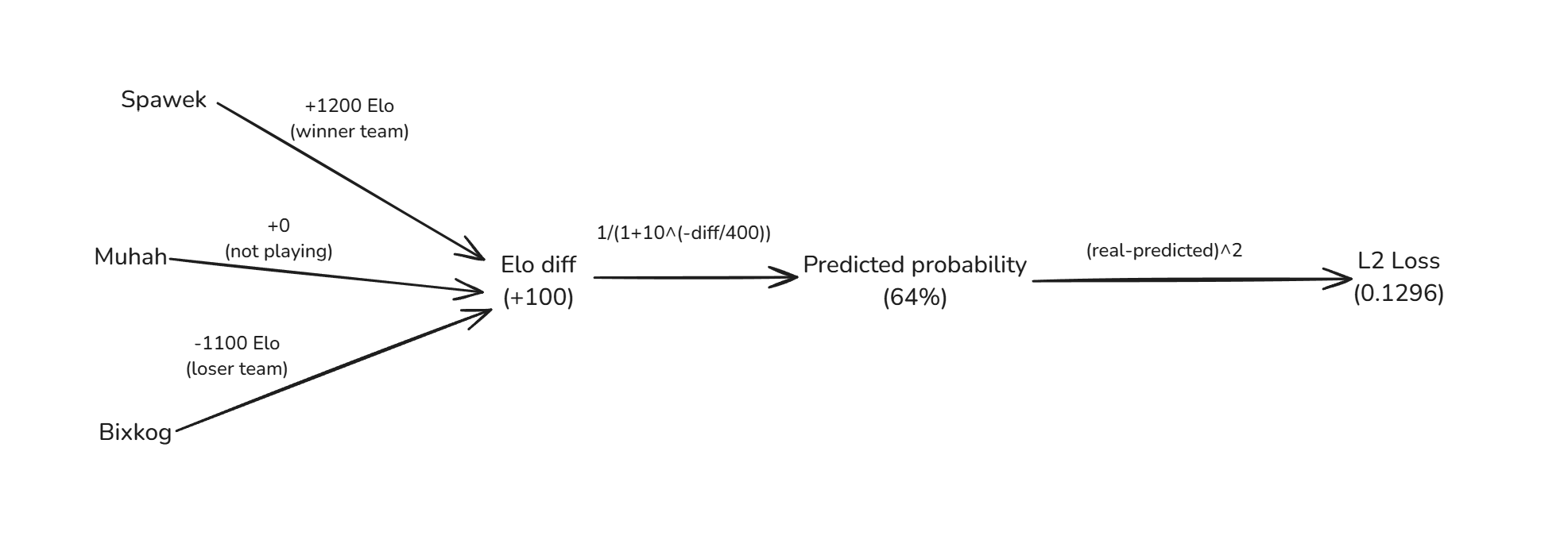
We defined the model defined. Now we need to train it somehow.
In each step backpropagation will help us move the Elo of each player to minimize the loss. It basically computes (through derivatives) how changing the Elo of each player will impact the loss.
First, we need to do a forward pass (computations we did on the last diagram) to compute loss, then we will move backward. We don't really need the loss itself, but we need it's derivative: $$ loss = (real - predicted) ^ 2 $$ $$ loss' = 2 * (real - predicted) $$
Then we multiply the result of that step by the derivative of the next step - win probability: $$ P(D) = \frac{1}{1 + 10^{\frac{-D}{400}}} $$ I used Wolfram Alpha to compute derivative:
$$ P(D)' = \frac{log(10)}{400*(1 + 10^{D/400})} - \frac{log(10)}{400*(1 + 10^{D/400})^2}$$
In the last step, we just add/subtract the Elo of each player depending on their team:
from collections import defaultdict
import math
def backpropagation(data, elo):
derivative = defaultdict(lambda: 0.0)
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
elo_diff = winner_elo - loser_elo
computed_probability = win_probability(winner_elo, loser_elo)
real_probability = 1.0
final_derivative = 2.0 * (real_probability - computed_probability)
win_probability_derivative = final_derivative * (
-math.log(10) / (400.0 * (1.0 + 10.0**(elo_diff / 400.0))**2)
+ math.log(10.0) / (400.0 * (1.0 + 10.0**(elo_diff / 400.0))))
for player in game["winner"]:
derivative[player] += win_probability_derivative
for player in game["loser"]:
derivative[player] -= win_probability_derivative
return derivative
We can directly use the backpropagation function to optimize our model:
from collections import defaultdict
LEARNING_RATE = 10_000.0
ITERATIONS = 10001
elo = defaultdict(lambda: 1000.0)
for i in range(0, ITERATIONS):
derivative = backpropagation(data, elo)
for player in derivative:
elo[player] += derivative[player] * LEARNING_RATE
The model managed to minimize the loss:
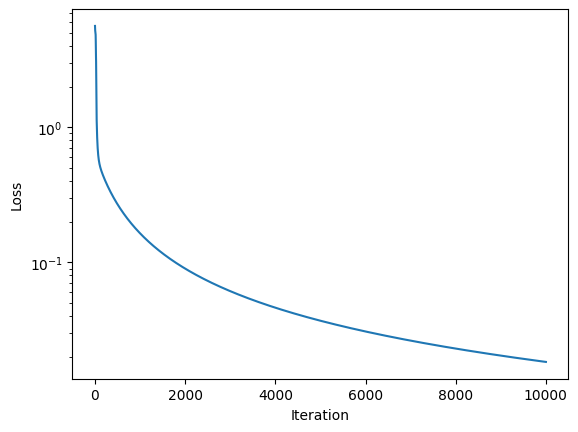
But the resulting Elo doesn't converge:
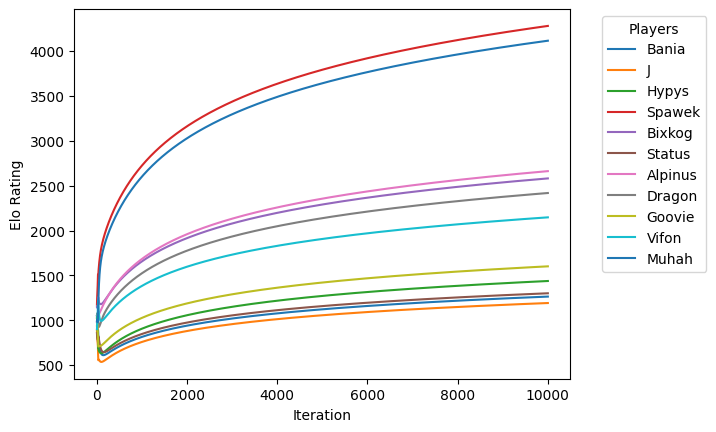
A quick peek at the data shows the reason: the model loss is very small and the model is overfitting. It basically learned all the games by heart and does not generalize.
Game:
winner elo: 9591, winner team: ['Bania', 'J', 'Spawek', 'Bixkog', 'Dragon']
loser elo: 7485, loser team: ['Hypys', 'Status', 'Alpinus', 'Goovie', 'Vifon']
computed probability: 0.999994567526197
real probability: 1
Game:
winner elo: 9964, winner team: ['Spawek', 'Bixkog', 'Status', 'Goovie', 'Dragon']
loser elo: 9431, loser team: ['J', 'Hypys', 'Alpinus', 'Vifon', 'Muhah']
computed probability: 0.9555615730980401
real probability: 1
Game:
winner elo: 9990, winner team: ['Hypys', 'Spawek', 'Bixkog', 'Alpinus', 'Bania']
loser elo: 9130, loser team: ['Status', 'Dragon', 'Muhah', 'J', 'Vifon']
computed probability: 0.9929703085603608
real probability: 1
(32 more games)
We have to solve this problem. The reason for which we create that model is to be able to construct good teams, not encode the history!
To fight overfitting we could go with typical ML solutions: we could add L1/L2 regularization or add some noise to the input data.
But I have another idea! We should remember that the historical games were mostly good - quite even Dota 2 games. Playing many games with same teams would probably lead to one team winning more often, but definitely not winning 100% of games.
I fetched more data from the history to asses which games were "even" and, which were "clearly one-sided".
I set "even" games to have a win probability of 75%, and "clearly one-sided" games to have a win probability of 95%:
{
"winner": ["Bixkog", "Status", "Alpinus", "Muhah", "Vifon"],
"loser": ["Hypys", "Spawek", "Goovie", "Dragon", "Bania", "J"],
"win_probability": 0.75, # even
},
{
"winner": ["Spawek", "Bixkog", "Alpinus", "J", "Vifon"],
"loser": ["Hypys", "Status", "Goovie", "Dragon", "Muhah", "Bania"],
"win_probability": 0.95, # one-sided
},
(...)
Using that in the code instead of 100% probability will make it way harder for the model to learn all the games by heart: the Elo difference needed for 75% win probability is ~200, the Elo difference needed for 100% probability is in the range [~500, infinity].
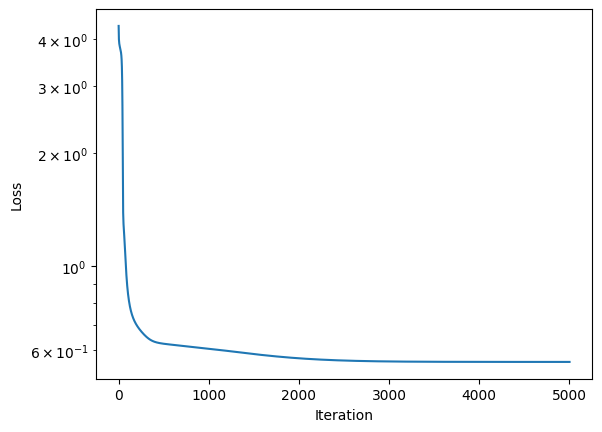
After updating the loss and backpropagation functions to use real_probability = game["win_probability"] instead of real_probability = 1 everything looks great.
Loss goes down quickly:
Players' Elo converge and are on reasonable levels:
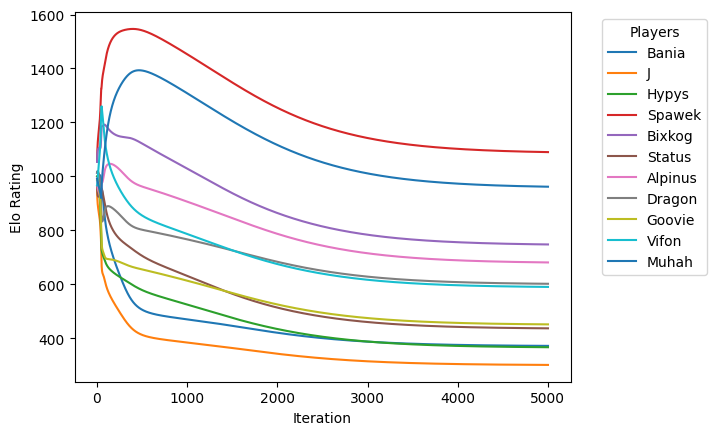
The new system is ready to predict victory chances, even with uneven team sizes. Here’s our first lineup for the LAN party starting in two weeks:
| team 1 (Elo: 2660) | team 2 (Elo: 2655) |
|---|---|
| Spawek | Hypys |
| Bixkog | Muhah |
| Bania | J |
| Goovie | Vifon |
| Status |
More updates to come!