
Siemanko! Jestem Spawek, a to historia projektu, który stworzyłem z przyjaciółmi, żeby usprawnić nasze LAN party.
Jeśli znasz angielski polecam: english version, bo ciężko mi przetłumaczyć wiele rzeczy - głównie techniczny żargon.
Od 16 lat organizujemy z ziomkami przynajmniej jedno LAN party każdego roku. Te imprezy trwają zwykle 4-5 dni, a w szczytowym momencie jest nas około 12 osób. To nie tylko granie - sporo imprezujemy, prowadzimy nerdowskie dyskusje, gramy w planszówki, karcianki jak Star Realms i w Mafię. Niektórzy przyjeżdżają później, inni wyjeżdżają wcześniej. Niektórzy wracają do domu na chwilę, aby zająć się dziećmi. LAN party to czas zabawy i relaksu.

To LAN party, więc sporo gramy na kompach! Głównie w Dota 2, ale też w klasyki jak Counter-Strike, Wolfenstein: Enemy Territory, Warcraft 3, Blooby Volley i inne.
Wybór drużyn - szczególnie do Doty 2 - zawsze był dla nas problemem. W trakcie LAN party postanowiliśmy zautomatyzować proces wyboru drużyn, co doprowadziło to do bardzo ciekawych pomysłów i zgrabnego rozwiązania. Ale aby to zrozumieć, potrzebujesz trochę kontekstu.
Pojedynczy mecz Doty 2 trwa około 40 minut i zazwyczaj rozgrywa się w formacie 5v5 (choć możliwe jest też 6v6). Niezbalansowane mecze, jak 4v5, zazwyczaj są bardzo jednostronne. W trakcie LAN party chcemy, żeby wszyscy brali udział w grze, więc często gry są niezbalansowane.
Lepsi gracze wykorzystują swoje umiejętności, aby szybciej zdobywać poziomy i zarabiać więcej złota przez co stają się jeszcze mocniejsi (tzw. snowball), co sprawia, że nawet niewielkie różnice między graczami stają się bardzo widoczne.
W naszej grupie około połowa z nas gra w Dotę regularnie, a reszta tylko podczas naszych LAN party, więc różnice w umiejętnościach są ogromne. Są też inne czynniki:
Zazwyczaj mamy dwóch liderów (typowo najlepszych lub najmniej doświadczonych graczy), którzy wybierają członków drużyny na przemian, podobnie jak przy wybieraniu drużyn do grania w gałę w szkole.
Mamy pewien trik: pierwszy lider wybiera jednego gracza, drugi wybiera dwóch, potem pierwszy lider dwóch, i tak dalej, ale w ostatniej turze każdy lider wybiera jednego gracza. Robimy to, żeby zmniejszyć przewagę pierwszego lidera.
Przykład dla 11 osób:
Leaders:
- Spawek (ja - lider 1)
- Bixkog (mój brat - lider 2)
1. wybór - drużyna 1 - 1. wybór = 1 gracz:
- Muhah
2. wybór - drużyna 2 - regularny wybór = 2 graczy:
- Alpinus
- Dragon
3. wybór - drużyna 1:
- Vifon
- Goovie
4. wybór - drużyna 2:
- Status
- Bania
5. wybór - drużyna 1 - ostatni wybór = 1 gracz:
- Hypys
6. wybór - drużyna 2 - ostatni wybór = 1 gracz:
- J
| drużyna 1 | drużyna 2 |
|---|---|
| Spawek | Bixkog |
| Muhah | Alpinus |
| Vifon | Dragon |
| Goovie | Status |
| Hypys | Bania |
| J |
Ze względu na duże różnice między graczami, ten proces prowadzi do podobnych lub nawet takich samych drużyn za każdym razem, co jest dla nas strasznie nudne. Gdy liczba graczy jest nieparzysta, zespoły wybrane w ten sposób są bardzo źle zrównoważone.
Podczas ostatniego LAN party byliśmy sfrustrowani i szybko napisaliśmy prosty kod, żeby wybierał drużyny za nas.
Znaleźliśmy trochę historycznych danych i wrzuciliśmy je do Colaba (wszystkie dane i kod tam są, jeśli chcesz się pobawić).
data = [
{
"winner": ["Dragon", "Spawek", "Status", "Vifon"],
"loser": ["Bixkog", "Alpinus", "Hypys", "J", "Goovie"]
},
{
"winner": ["Bixkog", "Alpinus", "Vifon", "J", "Goovie"],
"loser": ["Dragon", "Hypys", "Spawek", "Status"]
},
{
"winner": ["J", "Hypys", "Spawek", "Status", "Vifon"],
"loser": ["Bixkog", "Dragon", "Goovie", "Alpinus"]
},
# ... (35 gier w sumie)
]
Ranking Elo jest często używany w grach. Gracze zaczynają z 1000 punktami Elo, zdobywając lub tracąc punkty z każdą grą.
Prawdopodobieństwo, że P1 (gracz 1) wygra z P2, jest definiowane jako:
$$ P(P1, P2) = \frac{1}{1 + 10^{\frac{P2-P1}{400}}} $$
Tak więc jedynie różnica Elo między graczami (D) jest istotna:
$$ D = P1 - P2 $$
$$ P(D) = \frac{1}{1 + 10^{\frac{-D}{400}}} $$
Szansa na wygraną wynosi 50%, jeśli masz tyle samo punktów Elo co przeciwnik, 64%, jeśli masz o 100 punktów więcej, i 76%, jeśli masz o 200 punktów więcej:
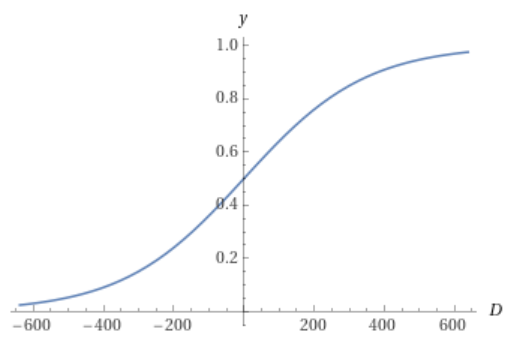
Aby uzyskać Elo każdej drużyny, po prostu sumujemy Elo wszystkich członków drużyny:
$$ Elo(drużyny) = \sum_{}^{team}Elo(gracza) $$
Oczywiście to problematyczne dla niezbalansowanych drużyn (np. 4v5), ale zacznijmy od czegoś prostego.
Stwórzmy pierwsze rozwiązanie, przyznając graczom 20 Elo za wygraną i odejmując 20 Elo za przegraną:
from collections import defaultdict
elo = defaultdict(lambda: 1000.0)
for game in data:
for winner in game["winner"]:
elo[winner] += 20.0
for loser in game["loser"]:
elo[loser] -= 20.0
Otrzymujemy następujące wyniki:
Spawek: 1260
Bixkog: 1140
Dragon: 1100
Bania: 1020
Muhah: 1020
Vifon: 1000
Hypys: 980
Alpinus: 960
Status: 900
Goovie: 900
J: 860
Dzięki temu możemy generować zbalansowane drużyny, znajdując kombinacje z najmniejszą różnicą Elo:
from itertools import combinations
requested_players = ["Hypys", "Spawek", "Bixkog", "Muhah", "J", "Vifon", "Bania", "Goovie"]
best_diff = float('inf')
best_team = None
expected_elo = sum([elo[player] for player in requested_players]) / 2
for team1 in combinations(requested_players, len(requested_players) // 2):
team1 = list(team1)
team1_elo = sum([elo[player] for player in team1])
diff = abs(team1_elo - expected_elo)
if diff < best_diff:
best_diff = diff
team2 = [player for player in requested_players if player not in team1]
team2_elo = sum([elo[player] for player in team2])
best_teams = (team1, team2, team1_elo, team2_elo)
print(f"team 1: {best_teams[0]}, total Elo: {round(best_teams[2])}")
print(f"team 2: {best_teams[1]}, total Elo: {round(best_teams[3])}")
Drużyny:
team 1: ['Hypys', 'Spawek', 'J', 'Vifon'], total Elo: 4100
team 2: ['Bixkog', 'Muhah', 'Bania', 'Goovie'], total Elo: 4080
Yay! Mamy pierwsze rozwiązanie!
Mamy tylko 35 historycznych gier, więc przejście przez nie tylko raz wydaje się marnotrawstwem.
W systemie Elo dostaniesz więcej niż 20 punktów, gdy wygrasz przeciwko graczowi o wyższym Elo, podobnie stracisz mniej niż 20 punktów, jeśli przegrasz z graczem o wyższym Elo. Dla zwycięzcy:
$$ update = 40 * (1 - P(win)) $$
Przegrany gracz traci dokładnie tyle samo punktów Elo, ile zdobywa zwycięzca. Na przykład:
Spawek (Elo: 1260) wygrywa z Goovie (Elo: 900):
Spawek += 4.47 Elo
Goovie -= 4.47 Elo
Status (Elo: 900) wygrywa z Dragon (Elo: 1100):
Status += 30.38 Elo
Dragon -= 30.38 Elo
W Colabie:
def win_probability(A, B):
elo_diff = A - B
return 1.0 / (1.0 + pow(10.0, (-elo_diff / 400.0)))
def elo_update(winner, loser):
prob = win_probability(winner, loser)
return 40.0 * (1 - win_probability(winner, loser))
Ponieważ używamy drużynowego Elo zamiast indywidualnego Elo graczy, podzielmy aktualizację równomiernie między wszystkich graczy w drużynie. Przeprowadźmy wielokrotne przejścia przez dane i zobaczmy, jak zmieniają się wyniki:
from collections import defaultdict
elo = defaultdict(lambda: 1000.0)
for iteration in range(0, 401):
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
update = elo_update(winner_elo, loser_elo)
for winner in game["winner"]:
elo[winner] += update / len(game["winner"])
for loser in game["loser"]:
elo[loser] -= update / len(game["loser"])
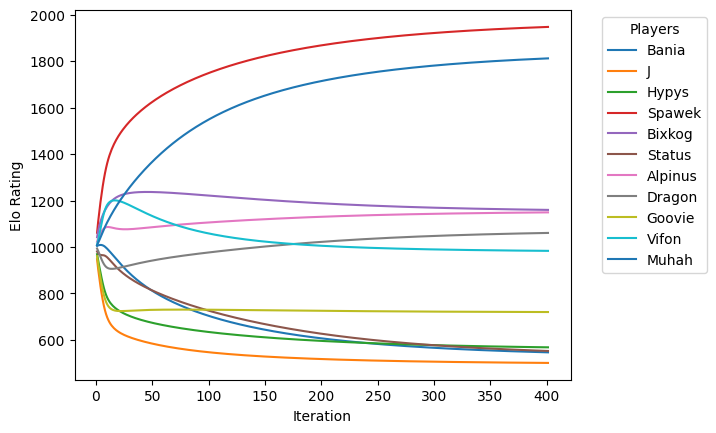
Napisaliśmy to podczas LAN party i było to naprawdę niesamowite uczucie widzieć, że wyniki się stabilizują! Korzystaliśmy z tego algorytmu do końca imprezy, dodając nowe dane po każdej grze.
Rozwiązanie było całkiem dobre, ale czasami generowało wyraźnie niezbalansowane mecze. W takich przypadkach po prostu dodawaliśmy mecz z domniemanym zwycięzcą do danych jako "fałszywą grę" i generowaliśmy nowe drużyny.
Wiedziałem, że do następego LAN party możemy zrobić to lepiej.
Kluczowe pomysły:
Pozostańmy przy systemie Elo, którego używamy. Model obliczy Elo dla każdego gracza. Porównamy SUM(Elo) drużyn, aby obliczyć prawdopodobieństwo wygranej.
Zdefiniujmy prostą funkcję L2 loss (loss = strata, to co chcemy zminimalizować). Nasz model będzie próbował zminimalizować stratę dla wszystkich gier: $$ loss = (\text{real_chance} - \text{predicted_chance})^2 $$
def loss(data, elo):
loss = 0.0
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
computed_probability = win_probability(winner_elo, loser_elo)
real_probability = 1.0
loss += (real_probability - computed_probability)**2.0
return loss
Więc aby obliczyć całkowitą stratę musimy przejść przez wszystkie gry i:
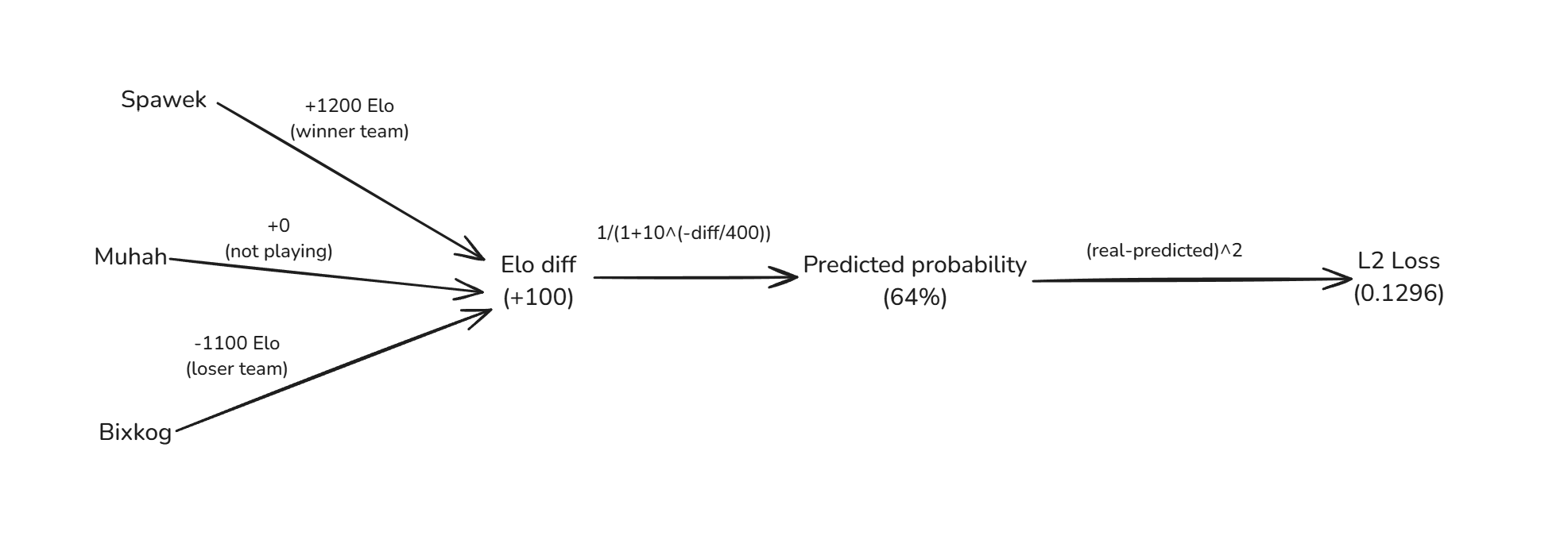
Zdefiniowaliśmy model. Teraz musimy go jakoś wytrenować.
W każdym kroku backpropagacja pomoże nam przesunąć Elo każdego gracza, aby zminimalizować stratę. Oblicza (przez pochodne), jak zmiana Elo każdego gracza wpłynie na stratę.
Najpierw musimy zrobić forward pass (obliczenia z ostatniego diagramu), aby obliczyć stratę, a potem przechodzimy wstecz. Właściwie nie potrzebujemy samej straty, ale jej pochodnej: $$ loss = (real - predicted) ^ 2 $$ $$ loss' = 2 * (real - predicted) $$
Następnie mnożymy wynik tego kroku przez pochodną kolejnego kroku - prawdopodobieństwa wygranej: $$ P(D) = \frac{1}{1 + 10^{\frac{-D}{400}}} $$ Użyłem Wolfram Alpha, aby obliczyć pochodną:
$$ P(D)' = \frac{log(10)}{400*(1 + 10^{D/400})} - \frac{log(10)}{400*(1 + 10^{D/400})^2}$$
W ostatnim kroku po prostu dodajemy/odejmujemy Elo każdego gracza w zależności od drużyny:
from collections import defaultdict
import math
def backpropagation(data, elo):
derivative = defaultdict(lambda: 0.0)
for game in data:
winner_elo = sum(elo[player] for player in game["winner"])
loser_elo = sum(elo[player] for player in game["loser"])
elo_diff = winner_elo - loser_elo
computed_probability = win_probability(winner_elo, loser_elo)
real_probability = 1.0
final_derivative = 2.0 * (real_probability - computed_probability)
win_probability_derivative = final_derivative * (
-math.log(10) / (400.0 * (1.0 + 10.0**(elo_diff / 400.0))**2)
+ math.log(10.0) / (400.0 * (1.0 + 10.0**(elo_diff / 400.0))))
for player in game["winner"]:
derivative[player] += win_probability_derivative
for player in game["loser"]:
derivative[player] -= win_probability_derivative
return derivative
Możemy bezpośrednio użyć funkcji backpropagation, aby zoptymalizować nasz model:
from collections import defaultdict
LEARNING_RATE = 10_000.0
ITERATIONS = 10001
elo = defaultdict(lambda: 1000.0)
for i in range(0, ITERATIONS):
derivative = backpropagation(data, elo)
for player in derivative:
elo[player] += derivative[player] * LEARNING_RATE
Modelowi udało się zminimalizować stratę:
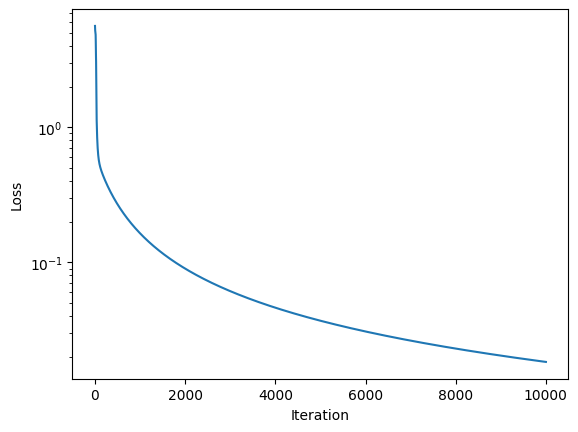
Ale wynikowe Elo się nie stabilizują:
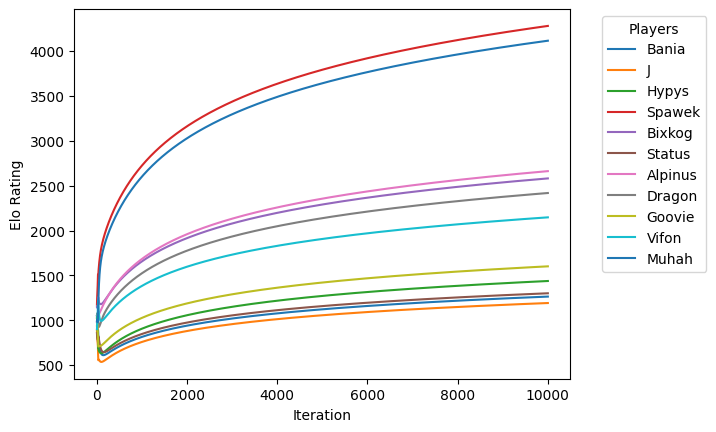
Krótki rzut oka na dane pokazuje przyczynę: strata modelu jest bardzo mała, a model jest przeuczony. W zasadzie nauczył się wszystkich gier na pamięć i nie generalizuje.
Gra:
elo zwycięzcy: 9591, drużyna zwycięska: ['Bania', 'J', 'Spawek', 'Bixkog', 'Dragon']
elo przegranego: 7485, drużyna przegrana: ['Hypys', 'Status', 'Alpinus', 'Goovie', 'Vifon']
prawdopodobieństwo wygranej: 0.999994567526197
realne prawdopodobieństwo: 1
Gra:
elo zwycięzcy: 9964, drużyna zwycięska: ['Spawek', 'Bixkog', 'Status', 'Goovie', 'Dragon']
elo przegranego: 9431, drużyna przegrana: ['J', 'Hypys', 'Alpinus', 'Vifon', 'Muhah']
prawdopodobieństwo wygranej: 0.9555615730980401
realne prawdopodobieństwo: 1
Gra:
elo zwycięzcy: 9990, drużyna zwycięska: ['Hypys', 'Spawek', 'Bixkog', 'Alpinus', 'Bania']
elo przegranego: 9130, drużyna przegrana: ['Status', 'Dragon', 'Muhah', 'J', 'Vifon']
prawdopodobieństwo wygranej: 0.9929703085603608
realne prawdopodobieństwo: 1
(32 inne gry)
Musimy rozwiązać ten problem. Powodem, dla którego tworzymy ten model, jest możliwość tworzenia dobrych drużyn, a nie zapamiętanie historii!
Aby walczyć z przeuczeniem, moglibyśmy użyć typowych rozwiązań ML: dodać regularizację L1/L2 lub dodać szum do danych wejściowych.
Mam lepszy pomysł! Powinniśmy pamiętać, że historyczne gry były głównie dobre - dość wyrównane mecze Doty 2. Grając wiele gier z tymi samymi drużynami, prawdopodobnie jedna drużyna wygrałaby więcej razy, ale zdecydowanie nie wygrywałaby 100% gier.
Zebrałem więcej danych z historii, aby ocenić, które gry były "wyrównane", a które były "jednostronna".
Ustawiłem prawdopodobieństwo wygranej na 75% dla "wyrównanych" gier i na 95% dla "jednostronnych" gier:
{
"winner": ["Bixkog", "Status", "Alpinus", "Muhah", "Vifon"],
"loser": ["Hypys", "Spawek", "Goovie", "Dragon", "Bania", "J"],
"win_probability": 0.75, # wyrównana
},
{
"winner": ["Spawek", "Bixkog", "Alpinus", "J", "Vifon"],
"loser": ["Hypys", "Status", "Goovie", "Dragon", "Muhah", "Bania"],
"win_probability": 0.95, # jednostronna
},
(...)
Użycie tego w kodzie zamiast 100% prawdopodobieństwa znacznie utrudni modelowi naukę wszystkich gier na pamięć: różnica Elo potrzebna do 75% prawdopodobieństwa wygranej to ~200, a różnica Elo potrzebna do 100% prawdopodobieństwa to od około ~500 do nieskończonoci.
Po aktualizacji funkcji loss i backpropagation, aby używały real_probability = game["win_probability"] zamiast real_probability = 1, wszystko wygląda świetnie.
Strata szybko spada:
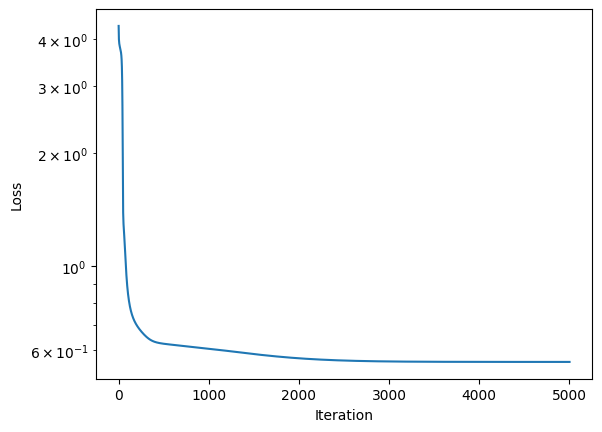
Elo graczy konwerguje i jest na rozsądnym poziomie:
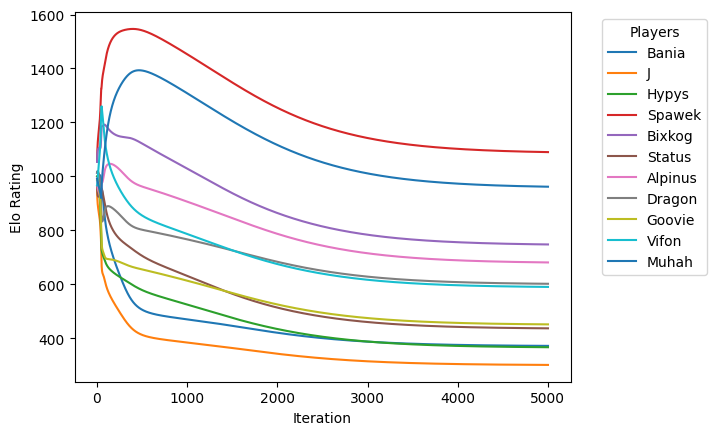
Nowy system jest gotowy do przewidywania szans na zwycięstwo, nawet przy nierównych rozmiarach drużyn. Oto nasz pierwszy skład na LAN party rozpoczynające się za dwa tygodnie:
| drużyna 1 (Elo: 2660) | drużyna 2 (Elo: 2655) |
|---|---|
| Spawek | Hypys |
| Bixkog | Muhah |
| Bania | J |
| Goovie | Vifon |
| Status |